Label Mixup vs Loss Mixup

Instead of mixing the labels as in classical mixup, mixing the losses might be more sensible for certain applications like speech enhancement.

Mixup

Minimizing a loss function on examples in the training set, also known as Empirical Risk Minimization (ERM), is the long established learning paradigm for supervised learning. Departing from tradition, mixup is a novel paradigm that proposes to train deep networks on virtual examples randomly sampled from the space of convex combinations of a pair of labeled examples.

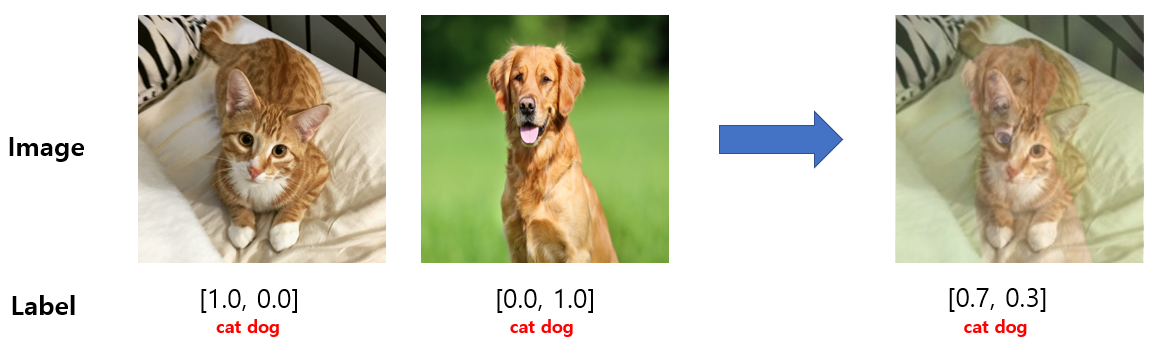
For random \(x_1,x_2\in\mathcal{X},y_1,y_2\in\mathcal{Y},\lambda\in[0,1]\), mixup creates the virtual example \((\lambda x_1 + (1-\lambda)x_2, \lambda y_1 + (1-\lambda)y_2)\) for training. Below, we show an interpolation of a cat and a dog image, credits to https://hoya012.github.io/blog/Bag-of-Tricks-for-Image-Classification-with-Convolutional-Neural-Networks-Review/.

Applying Mixup Beyond Classification

Mixup has been shown to boost generalization and calibration when used to train deep networks on classification tasks. However, it is not clear how to generalize it to tasks beyond classification.

Here are two possibilities:

1) Label mixup: \(\mathcal{L}(\hat{y}, \lambda y_1 + (1-\lambda) y_2)\)

2) Loss mixup: \(\lambda \mathcal{L}(\hat{y}, y_1) + (1-\lambda) \mathcal{L}(\hat{y}, y_2)\)

Mixing the labels seems like the obvious way, since this is how mixup was originally formulated. But it turns out that mixing the losses is also a valid generalization, because it is equivalent to mixing the losses for classification tasks.

The theorem implies that label and loss mixup are equivalent for the cross-entropy and mean squared error losses, which are most commonly used respectively in classification and regression.

Example of Speech Enhancement

In general, however, the two mixups have very different effects. For a task like speech enhancement, where we train a network to map from a noisy speech sample to a clean one, the two versions of mixup lead to two vastly different interpretations.

Label mixup results in training against a noisy target, since the mix of two clean samples becomes a noisy one. By contrast, loss mixup results in an implicit solution of the cocktail party problem, where we train a network to extract each individual clean signal from a mix of two noisy samples.

Indeed, our experimental results reveal that loss mixup leads to superior performance compared to ERM, but not label mixup.

Thus, when applying mixup to non-classification tasks, it helps to think carefully about the qualitative difference between label and loss mixup before choosing the appropriate one.

For more insights about mixup (for example, using the reparametrization trick to tune the mixing distribution), please check out our paper.